|
|
#1 (permalink) |
|
Member
Регистрация: 22.10.2016
Сообщений: 62
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 10
|
L = a*(2.28 * (b/a) ^ 1.44 + 4). Относительная погрешность составляет величину порядка 0,5% Мне нужно, чтобы кто-то подтвердил или опроверг эту формулу. прилагаю программу на QBasic, которая и просчитала погрешность, вычисляя длину эллипса методом трапеций и по формуле. Код:
REM QBASIC
DECLARE FUNCTION p! (b!)
DECLARE FUNCTION f! (b!)
CLS
SCREEN 11
WINDOW (-.5, 6.5)-(1.5, 3.5)
LINE (0, 4)-(0, 6.2832)
LINE (1, 4)-(1, 6.2832)
LINE (0, 4)-(1, 4)
LINE (0, 6.2832)-(1, 6.2832)
FOR b = 0 TO 1 STEP .005
PSET (b, f(b))
PSET (b, p(b))
NEXT b
FOR b = 0 TO 1.01 STEP .05
PRINT USING "##.## %"; (f(b) - p(b)) / f(b) * 100
NEXT b
SLEEP 0
SCREEN 0
END
FUNCTION f (b)
h = .002
s = (b + 1) / 2
FOR x = h TO 1.57 STEP h
s = s + SQR(SIN(x) ^ 2 + (b * COS(x)) ^ 2)
NEXT x
f = 4 * h * s
END FUNCTION
FUNCTION p (b)
p = 2.28 * b ^ 1.44 + 4
END FUNCTION
|
|
|

|
|
|
|
|
Helpmaster
Member
Регистрация: 08.03.2016
Сообщений: 0
|
Почитайте так же аналогичные темы, если есть свободная минутка Формула расчета длины фазоинвертора. Верна ли она? Формула-1 |
|
|
#2 (permalink) | |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
Цитата:
Здесь я могу предложить более простой и точный метод. Длина (периметр) эллипса вычисляется, как L = 4*a*E(m), где m² = (a² - b²)/a², а Е(m) - полный эллиптический интеграл второго рода. Он может быть с точностью до пятого знака аппроксимирован функцией E(m) = [1 + a1*n + a2*n²] + [b1*n + b2*n²]*ln(1/n), где n = 1 - m, а коэффициенты имеют следующие значения: a1 = 0.4630151 a2 = 0.1077812 b1 = 0.2452727 b2 = 0.0412496 |
|
|
|

|
|
|
#5 (permalink) |
|
Member
Регистрация: 22.10.2016
Сообщений: 62
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 10
|
Vladimir_S,
Вы понимаете, крайние значения были заданы по умолчанию точно. То есть большая п-ось а была положена равной 1 и потому крайние значения должны были равны 4 и 6,2832... Поскольку получилась функция от одной переменной b (малая п-ось), то несложно было вычислить и длину эллипса. График длины эллипса показал, что это степенная функция. И осталось вычислить только степень.... Спасибо вам за формулу! |
|
|

|
| Ads | |
|
Member
Регистрация: 31.10.2006
Сообщений: 40200
Записей в дневнике: 0
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 55070
|
|
|
|
#6 (permalink) |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
Что-то как-то у меня не очень хороший результат получился с Вашей аппроксимацией... Если не наврал, то так:
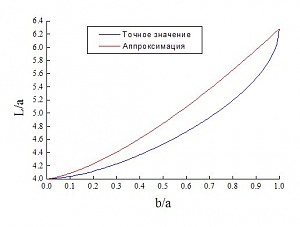 В области наибольшего расхождения погрешность достигает 8.5%. Многовато. На всякий случай - вот программа (увы, Паскаль, а не Бэйсик): Код:
Var f:Text; i:Byte; r:Real; Const a1 = 0.4630151; a2 = 0.1077812; b1 = 0.2452727; b2 = 0.0412496; Function Ell_Int(ba:real):real; var n,m:real; begin m:=SQRT(1-Sqr(ba)); n:=1-m; Ell_Int:=((1+a1*n+a2*n*n)+(b1*n + b2*n*n)*ln(1/n))*4; end; Function Ell_App(ba:real):real; begin Ell_App:=((Pi*2-4)*Exp(1.44*ln(ba))+4); end; Begin Assign(f,'D:\Ell.dat'); Rewrite(f); for i:=1 to 100 do begin r:=0.01*i; writeln(f,r:4:2,Ell_Int(r):15:5,Ell_App(r):15:5,Abs((Ell_App(r)-Ell_Int(r))/(Ell_App(r)+Ell_Int(r)))*200:15:5); end; Close(f); End. |
|
|

|
|
|
#7 (permalink) |
|
Member
Регистрация: 22.10.2016
Сообщений: 62
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 10
|
Vladimir_S
довольно сложно понять эллиптический интеграл, когда с ним не имеешь дела. У меня все было проще. Вот формула эллипса в параметрическом виде x = a*cos(t) , (a = 1) y = b*sin(t) отсюда легко определяется дифференциал дуги и вычисляется длина эллипса... Вот два графика - они практически сливаются в одну линию. Слева столбец - расчет относительной погрешности в процентах. |
|
|

|
|
|
#8 (permalink) |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
Да, виноват: где-то лажа. Или у меня (что скорее), или в справочнике по спецфункциям. Сейчас посчитал Вашим методом (правда, по Симпсону, причем до схождения в третьем знаке) - всё сошлось с Вашей аппроксимацией. Разберусь на досуге, где ошибка - аж самому интересно:

|
|
|

|
|
|
#9 (permalink) |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
М-да, пока - непонятно. Склоняюсь к тому, что в справочнике лажа. А ведь уж ЭТОМУ труду привык верить, как себе...
|
|
|

|
| Ads | |
|
Member
Регистрация: 31.10.2006
Сообщений: 40200
Записей в дневнике: 0
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 55070
|
|
 |
|
|