|
|
#1 (permalink) |
|
Member
Регистрация: 14.06.2010
Сообщений: 911
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 353
|
1. Центр окружности лежит не в точке начала координат, определить лежит ли данная точка (координаты с клавиатуры) внутри окружности и вывести ответ в виде yes\no. 2.Тоже самое, только вместо окружности - прямоугольник 3. вместо окружности - неправильный многоугольник (любой) |
|
|

|
|
|
|
|
Helpmaster
Member
Регистрация: 08.03.2016
Сообщений: 0
|
Рекомендую обратить внимание на данные топики, в них могут быть полезные ответы Программы Интересные программы Программы для тестов ПК |
|
|
#2 (permalink) |
|
support
Регистрация: 19.08.2007
Адрес: Зея
Сообщений: 15,797
Записей в дневнике: 71
Сказал(а) спасибо: 166
Поблагодарили 203 раз(а) в 86 сообщениях
Репутация: 75760
|
Во всех трех заданиях - как задаются исходные фигуры? Для определения принадлежности необходимо знать исходные координаты и другие параметры фигур.
1) Принадлежность точки определяем, исходя из уравнения окружности. 2) Принадлежность точки определяем, сравнивая соответствующие координаты с координатам сторон прямоугольника. 3) Описываем каждую сторону многоугольника уравнением прямой, последовательно определяем принадлежность точки, сравнивая введенные координаты с допустимыми.
__________________
Убить всех человеков! |
|
|

|
|
|
#5 (permalink) |
|
Member
Регистрация: 14.06.2010
Сообщений: 911
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 353
|
Ааааа, завтра сдавать!!!!
|
|
|

|
| Ads | |
|
Member
Регистрация: 31.10.2006
Сообщений: 40200
Записей в дневнике: 0
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 55070
|
|
|
|
#6 (permalink) |
|
support
Регистрация: 19.08.2007
Адрес: Зея
Сообщений: 15,797
Записей в дневнике: 71
Сказал(а) спасибо: 166
Поблагодарили 203 раз(а) в 86 сообщениях
Репутация: 75760
|
Объясните, как фигура может быть константой? Любая плоская фигура задаётся в какой-либо плоскости, соответственно, в другой плоскости проекция фигуры может по форме не совпадать с исходной, поэтому о постоянстве в геометрии не может быть и речи
 . Полагаю, что вы имели в виду постоянство координат вершин фигуры в данной плоскости. . Полагаю, что вы имели в виду постоянство координат вершин фигуры в данной плоскости.Предлагаю такой вариант решения: 1) Разбиваем многоугольник на конечное число трапеций, причем две противоположные стороны должны быть параллельными на первом этапе анализа оси абсцисс, на втором этапе - оси ординат. Обратите внимание, что при разбиении могут появиться треугольники. 2) Проверяем попадание абсциссы заданной точки внутрь каждой трапеции или треугольника. Учитываем при анализе, что совпадение координаты с одной из точек стороны трапеции также говорит о попадании. 3) Также проверяем попадание абсциссы заданной точки. 4) Делаем общий вывод о принадлежности данной точки заданной фигуре. 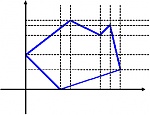
|
|
|

|
|
|
#8 (permalink) |
|
support
Регистрация: 19.08.2007
Адрес: Зея
Сообщений: 15,797
Записей в дневнике: 71
Сказал(а) спасибо: 166
Поблагодарили 203 раз(а) в 86 сообщениях
Репутация: 75760
|
Если взять горизонталь за OX, а вертикаль - за OY, вполне можно составить каноническое уравнение любой прямой, содержащей отрезок, ограниченный двумя вершинами многоугольника.
Прямая — Википедия
__________________
Убить всех человеков! |
|
|

|
|
|
#9 (permalink) |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
Я вот поразмыслил над этой задачкой, и пришел мне в голову такой алгоритм:
нужно отрезками прямых соединить точку со всеми вершинами и сосчитать сумму углов между всеми парами смежных лучей, выходящих из нашей точки. Если эта сумма составит 360°, то точка - внутренняя, если нет - наружная. К сожалению, на реализацию такой программы уже нет ни времени, ни сил. |
|
|

|
|
|
#10 (permalink) |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
|
|
|

|
| Ads | |
|
Member
Регистрация: 31.10.2006
Сообщений: 40200
Записей в дневнике: 0
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 55070
|
|
 |
|
|