|
||||||||
| Главная | Правила | Регистрация | Дневники | Справка | Пользователи | Календарь | Поиск | Сообщения за день | Все разделы прочитаны |
 |
|
|
Опции темы | Опции просмотра |
|
||||||||
| Главная | Правила | Регистрация | Дневники | Справка | Пользователи | Календарь | Поиск | Сообщения за день | Все разделы прочитаны |
 |
|
|
Опции темы | Опции просмотра |
|
|
#1 (permalink) |
|
Новичок
Регистрация: 11.03.2015
Сообщений: 2
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 10
|
Для функции разработать и протестировать программу, выполняющую: 1.нахождение всех действительных корней уравнения на отрезке [a; b], если таковые имеются (решение соответствующего уравнения выполнить с точностью до e=0,0001 одним из численных методов: хорд, не более, чем за 20 итераций. 2. вычисление определенного интеграла f(x) на интервале табулирования [a; b] одним из перечисленных методов: правых прямоугольников. x^4 + 0.5x^3 – 4x^2 – 3x – 0.5 = 0 интервал [–1, 0] Заранее спасибо. |
|
|

|
|
|
|
|
Helpmaster
Member
Регистрация: 08.03.2016
Сообщений: 0
|
Подобные темы уже встречались на форуме, пролистайте их Программирование функции 1/х Разработать программу шифрования текстовых файлов, Паскаль Разработать программу в среде Delphi Разработать программу с использованием и без использовая динамических структур данных Программирование функции |
|
|
#2 (permalink) | |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
Цитата:
Вопрос о методах численного решения алгебраических уравнений подробно рассмотрен здесь: К вопросу о численном решении алгебраических уравнений Как там и сказано, начнем с анализа функции с целью определения количества корней и их приближенно-грубых значений, для чего построим график в указанном интервале: 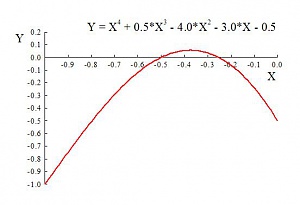 Как видно из графика, есть два корня, приблизительно равные -0.5 и -0.25. Точные значения их будем искать в интервалах [-0.6; -0.4] и [-0.3; -0.2], соответственно. Ну и вот программа: Код:
Const
Eps=0.0001;
a=-1.0;
b=0.0;
Var
Res:Real;
N:Integer;
Function F(z:real):Real;
begin
F:=Sqr(Sqr(z))+0.5*z*Sqr(z)-4.0*Sqr(z)-3.0*z-0.5;
end;
Function Antiderivative(Q:real):Real;
begin
Antiderivative:=0.2*Q*Sqr(Sqr(Q))+0.125*Sqr(Sqr(Q))-(4.0/3)*Q*Sqr(Q)-1.5*Sqr(Q)-0.5*Q;
end;
Procedure EQRoot(a1,b1:real; var R:real; var m:Integer);
var
x1,x2,d,c:real;
k:Integer;
begin
k:=0;
c:=a1;
x1:=b1;
Repeat
x2:=x1-F(x1)*(x1-c)/(F(x1)-F(c));
d:=abs(x1-x2);
x1:=x2;
Inc(k);
Until d<Eps;
R:=x2;
m:=k;
end;
Procedure Integral(var R:Real; var m:Integer);
var
h,S1,S2,d:real;
p,k,i:Integer;
begin
k:=0;
p:=10;
S1:=0;
h:=(b-a)/p;
for i:=0 to p-1 do S1:=S1+h*F(a+h*i);
repeat
S2:=0;
p:=p+10;
Inc(k);
h:=(b-a)/p;
for i:=0 to p-1 do S2:=S2+h*F(a+h*i);
d:=Abs(S2-S1);
S1:=S2;
until d<Eps;
R:=S2;
m:=k;
end;
Begin
Writeln('Roots: ');
EQRoot(-0.6,-0.4,Res,N);
Writeln('X1 = ',Res:8:5,', ',N,' iterations');
EQRoot(-0.3,-0.2,Res,N);
Writeln('X2 = ',Res:8:5,', ',N,' iterations');
Writeln;
Writeln('Integral:');
Writeln('Numerical:');
Integral(Res,N);
Writeln(Res:0:5,', ',N,' iterations');
Writeln('Accurate:');
Writeln((Antiderivative(b)-Antiderivative(a)):0:5);
Readln
End.

|
|
|
|

|
|
|
#4 (permalink) |
|
Специалист
Регистрация: 27.08.2008
Адрес: Санкт-Петербург
Сообщений: 27,807
Сказал(а) спасибо: 340
Поблагодарили 583 раз(а) в 208 сообщениях
Репутация: 113184
|
|
|
|

|
| Ads | |
|
Member
Регистрация: 31.10.2006
Сообщений: 40200
Записей в дневнике: 0
Сказал(а) спасибо: 0
Поблагодарили 0 раз(а) в 0 сообщениях
Репутация: 55070
|
|
 |
| Опции темы | |
| Опции просмотра | |
|
|